Green function for a non-Markovian Fokker-Planck equation: Comb-model and anomalous diffusion

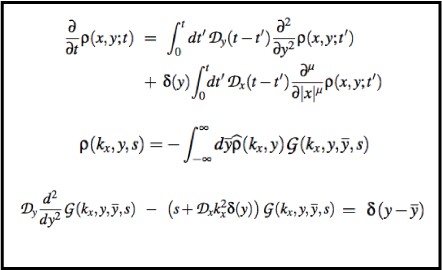
Abstract

We investigate solutions, by using the Green function approach, for a system governed by a non-Markovian Fokker-Planck equation and subjected to a Comb structure. This structure consists of the axis of structure as the backbone and fingers which are attached perpendicular to the axis. For this system, we consider an arbitrary initial condition, in the presence of time dependent diffusion coefficients and spatial fractional derivative, and analyze the connection to the anomalous diffusion.