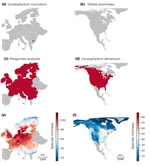
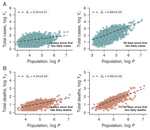
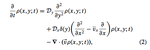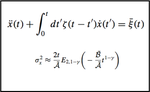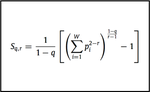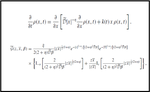Publications
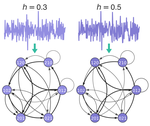
Nearest neighbor permutation entropy detects phase transitions in complex high-pressure systems
Understanding the high-pressure phase behavior of carbon dioxide-hydrocarbon mixtures is of considerable interest owing to their wide …
Structural roles and gender disparities in corruption networks
Criminal activities are predominantly due to males, with females exhibiting a significantly lower involvement, especially in serious …
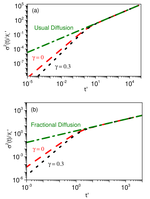
Diffusion in a comb-structured media: Non-local terms and stochastic resetting
We examine the dynamics of a system influenced by a backbone structure, incorporating linear non-local terms that account for both …
Two-by-two ordinal patterns in art paintings
Quantitative analysis of visual arts has recently expanded to encompass a more extensive array of artworks due to the availability of …
Diffusion in comb-structured surfaces coupled to bulk processes
From the analytical perspective, we investigate the diffusion processes that arise from a system composed of a surface with a backbone …
Impact of inter-city interactions on disease scaling
Inter-city interactions are critical for the transmission of infectious diseases, yet their effects on the scaling of disease cases …
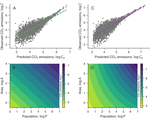
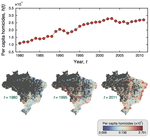
Urban carbon dioxide emissions and the roles of population, area, and density
This chapter revisits a generalized framework based on an analogy with the economic theory of production functions for simultaneously …
Density scaling laws and rural-to-urban transitions
This chapter revisits an attempt to incorporate rural and urban regions into a coherent and unified approach based on scaling …
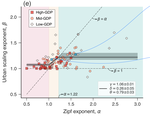
Connection between Zipf's law and urban scaling
This chapter revisits two approaches connecting Zipf’s law and urban scaling – two of the best-known examples of regularities emerging …
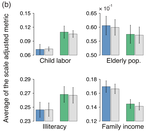
Comparing cities of different sizes with scale-adjusted metrics
Scaling laws between urban indicators and the population are one of the most striking and universal findings of recent urban studies. …
Quantifying the 15-minute city concept
Amid growing urbanization, the 15-minute city model seeks to transform city living by ensuring essential services are just a short walk …
Shape patterns in popularity series of video games
In recent years, digital games have become increasingly present in people’s lives both as a leisure activity or in gamified activities …
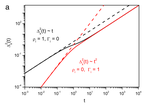
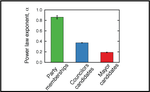
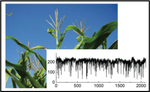
Characterizing unstructured data with the nearest neighbor permutation entropy
Permutation entropy and its associated frameworks are remarkable examples of physics-inspired techniques adept at processing complex …
A heteroscedastic Bayesian generalized logistic regression model with application to scaling problems
Power law scaling models have been used to understand the complexity of systems as diverse as cities, neurological activity, and …
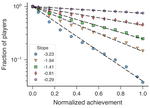
Complexity of popularity and dynamics of within-game achievements in computer games
Tasks of different nature and difficulty levels are a part of people’s lives. In this context, there is a scientific interest in the …
Universal productivity patterns in research careers
A common expectation is that career productivity peaks rather early and then gradually declines with seniority. But whether this holds …
Results for nonlinear diffusion equations with stochastic resetting
We investigate a nonlinear diffusion process in which particles stochastically reset to their initial positions at a constant rate. The …
Interplay between particle trapping and heterogeneity in anomalous diffusion
Heterogeneous media diffusion is often described using position-dependent diffusion coefficients and estimated indirectly through mean …
Complexity of the COVID-19 pandemic in Maringá
While extensive literature exists on the COVID-19 pandemic at regional and national levels, understanding its dynamics and consequences …
Deep learning criminal networks
Recent advances in deep learning methods have enabled researchers to develop and apply algorithms for the analysis and modeling of …
Age and market capitalization drive large price variations of cryptocurrencies
Cryptocurrencies are considered the latest innovation in finance with considerable impact across social, technological, and economic …
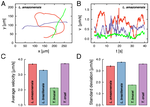
Effects of shady environments on fish collective behavior
Despite significant efforts devoted to understanding the underlying complexity and emergence of collective movement in animal groups, …
Machine Learning Partners in Criminal Networks
Recent research has shown that criminal networks have complex organizational structures, but whether this can be used to predict static …
Schrödinger Equation with Geometric Constraints and Position-Dependent Mass
We investigate the solutions of the Schrödinger equation in the presence of geometric constraints represented by a backbone structure …
Invasive alien species records are exponentially rising across the Earth
Humans are facilitating the introduction and range expansion of invasive alien species (IAS), which have negatively impacted ecological …
The Physics of Cities
The word “physics” can be understood in at least two ways. First, based on the Greek origin of the word, physics means …
On the dynamics of reporting data: A case study of UFO sightings
There are a growing number of large databases online. In this study, we used data from 80,332 cases of UFO sightings reported from 1906 …
Characterizing postural sway signals by the analysis of zero-crossing patterns
Center of pressure (COP) signals have been widely used to investigate various aspects of human balance during quiet standing. Here, we …
Popularity of Video Games and Collective Memory
Describing the permanence of cultural objects is an important step in understanding societal trends. A relatively novel cultural object …
Clustering free-falling paper motion with complexity and entropy
Many simple natural phenomena are characterized by complex motion that appears random at first glance, but that often displays …
Universality of political corruption networks
Corruption crimes demand highly coordinated actions among criminal agents to succeed. But research dedicated to corruption networks is …
Permutation Jensen-Shannon distance: A versatile and fast symbolic tool for complex time-series analysis
The main motivation of this paper is to introduce the permutation Jensen-Shannon distance, a symbolic tool able to quantify the degree …
Fractional Diffusion with Geometric Constraints: Application to Signal Decay in Magnetic Resonance Imaging (MRI)
We investigate diffusion in three dimensions on a comb-like structure in which the particles move freely in a plane, but, out of this …
Population Density and Spreading of COVID-19 in England and Wales
We investigated daily COVID-19 cases and deaths in the 337 lower tier local authority regions in England and Wales to better understand …
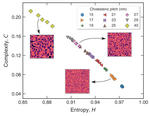
Determining liquid crystal properties with ordinal networks and machine learning
Machine learning methods are becoming increasingly important for the development of materials science. In spite of this, the use of …
Transient anomalous diffusion in heterogeneous media with stochastic resetting
We investigate a diffusion process in heterogeneous media where particles stochastically reset to their initial positions at a constant …
Commuting network effect on urban wealth scaling
Urban scaling theory explains the increasing returns to scale of urban wealth indicators by the per capita increase of human …
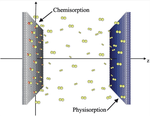
Sorption-Desorption, Surface diffusion, and Memory Effects in a 3D System
Bio and nature behaviors inspired modelling of diffusion and trapping of particles, key phenomena for life occurrence, must consider a …
Stationary solution and H theorem for a generalized Fokker-Planck equation
We investigate a family of generalized Fokker-Planck equations that contains Richardson and porous media equations as members. …
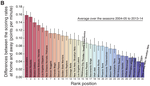
Association between productivity and journal impact across disciplines and career age
The association between productivity and impact of scientific production is a long-standing debate in science that remains …
ordpy: A Python package for data analysis with permutation entropy and ordinal network methods
Since Bandt and Pompe’s seminal work, permutation entropy has been used in several applications and is now an essential tool for time …
Little evidence of range size conservatism in freshwater plants across two continents
Aim Range size conservatism suggests that closely‐related species maintain geographic ranges of similar extent. However, consensus …
Association between population distribution and urban GDP scaling
Urban scaling and Zipf’s law are two fundamental paradigms for the science of cities. These laws have mostly been investigated …
Collective dynamics of stock market efficiency
Summarized by the efficient market hypothesis, the idea that stock prices fully reflect all available information is always confronted …
Mapping images into ordinal networks
An increasing abstraction has marked some recent investigations in network science. Examples include the development of algorithms that …
Rural-Urban Scaling of Age, Mortality, Crime and Property Reveals a Loss of Expected Self-Similar Behaviour
The urban scaling hypothesis has improved our understanding of cities; however, rural areas have been neglected. We investigated …
City size and the spreading of COVID-19 in Brazil
The current outbreak of the coronavirus disease 2019 (COVID-19) is an unprecedented example of how fast an infectious disease can …
Anomalous diffusion and sorption-desorption process in complex fluid systems
Diffusion processes occurring in a myriad of systems sparkle great interest in understanding their general properties and applications. …
Anomalous diffusion and random search in xyz-comb: exact results
We present an analytical treatment of anomalous diffusion in a three-dimensional comb (xyz-comb) by using the Green’s function …
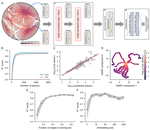
Learning physical properties of liquid crystals with deep convolutional neural networks
Machine learning algorithms have been available since the 1990s, but it is much more recently that they have come into use also in the …
Quenched and Annealed Disorder Mechanisms in Comb-Models with Fractional Operators
Recent experimental findings on anomalous diffusion have demanded novel models that combine annealed (temporal) and quenched (spatial …
Gender difference in candidature processes for Brazilian elections
Researchers of several areas have reported that there are still significant gender differences in their performances within different …
Extensions and Solutions for Nonlinear Diffusion Equations and Random Walks
We investigate a connection between random walks and nonlinear diffusion equations within the framework proposed by Einstein to explain …
Characterizing stochastic time series with ordinal networks
Approaches for mapping time series to networks have become essential tools for dealing with the increasing challenges of characterizing …
Effects of changing population or density on urban carbon dioxide emissions
The question of whether urbanization contributes to increasing carbon dioxide emissions has been mainly investigated via scaling …
Quantifying postural sway dynamics using burstiness and interevent time distributions
We propose an approach for analysing the dynamics of human postural sway using measures applied to study inhomogeneous temporal …
Anomalous diffusion behavior in parliamentary presence
Concepts of statistical mechanics as well as other typical tools of physics have been largely used in the analysis of several aspects …
Estimating physical properties from liquid crystal textures via machine learning and complexity-entropy methods
Imaging techniques are essential tools for inquiring a number of properties from different materials. Liquid crystals are often …
Clustering patterns in efficiency and the coming-of-age of the cryptocurrency market
The efficient market hypothesis has far-reaching implications for financial trading and market stability. Whether or not …
The hidden traits of endemic illiteracy in cities
In spite of the considerable progress towards reducing illiteracy rates, many countries, including developed ones, have encountered …
History of art paintings through the lens of entropy and complexity
Art is the ultimate expression of human creativity that is deeply influenced by the philosophy and culture of the corresponding …
A nonlinear Fokker–Planck equation approach for interacting systems: Anomalous diffusion and Tsallis statistics
We investigate the solutions for a set of coupled nonlinear Fokker–Planck equations coupled by the diffusion coefficient in presence of …
Robustness of sentence length measures in written texts
Hidden structural patterns in written texts have been subject of considerable research in the last decades. In particular, mapping a …
Crime prediction through urban metrics and statistical learning
Understanding the causes of crime is a longstanding issue in researcher’s agenda. While it is a hard task to extract causality from …
Nonlinear Diffusion Equation with Reaction Terms: Analytical and Numerical Results
We investigate a process obtained from a combination of nonlinear diffusion equations with reaction terms connected to a reversible …
Unveiling Relationships Between Crime and Property in England and Wales Via Density Scale-Adjusted Metrics and Network Tools
Scale-adjusted metrics (SAMs) are a significant achievement of the urban scaling hypothesis. SAMs remove the inherent biases of per …
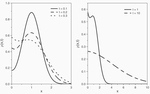
Characterization of Time Series Via Rényi Complexity-Entropy Curves
One of the most useful tools for distinguishing between chaotic and stochastic time series is the so-called complexity-entropy …
The dynamical structure of political corruption networks
Corruptive behaviour in politics limits economic growth, embezzles public funds, and promotes socio-economic inequality in modern …
The role of fractional time-derivative operators on anomalous diffusion
The generalized diffusion equations with fractional order derivatives have shown be quite efficient to describe the diffusion in …
Fractional Calculus in Electrical Impedance Spectroscopy: Poisson-Nernst-Planck model and Extensions
We review some analytical results obtained in the context of the fractional calculus for the electrical spectroscopy impedance, a …
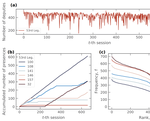
Power-law relaxation in human violent conflicts
We study relaxation patterns of violent conflicts after bursts of activity. Data were obtained from available catalogs on the conflicts …
Spatial patterns of dengue cases in Brazil
Dengue infection plays a central role in our society, since it is the most prevalent vector-borne viral disease affecting humans. We …
Characterizing Time Series via Complexity-Entropy Curves
The search for patterns in time series is a very common task when dealing with complex systems. This is usually accomplished by …
Random Walks Associated with Nonlinear Fokker–Planck Equations
A nonlinear random walk related to the porous medium equation (nonlinear Fokker–Planck equation) is investigated. This random walk is …
Ion Motion in Electrolytic Cells: Anomalous Diffusion Evidences
In this study, we argue that ion motion in electrolytic cells containing Milli-Q water, weak electrolytes, or liquid crystals may …
Intermittent Motion, Nonlinear Diffusion Equation and Tsallis Formalism
We investigate an intermittent process obtained from the combination of a nonlinear diffusion equation and pauses. We consider the …
Asymptotic behaviors of the Poisson-Nernst-Planck model, generalizations and best adjust of experimental data
We analyze the asymptotic behavior of the impedance (or immittance) spectroscopy response of an electrolytic cell in a finite-length …
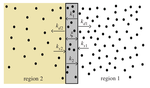
Anomalous diffusion and transport in heterogeneous systems separated by a membrane
Diffusion of particles in a heterogeneous system separated by a semipermeable membrane is investigated. The particle dynamics is …
Differences in Collaboration Patterns across Discipline, Career Stage, and Gender
Collaboration plays an increasingly important role in promoting research productivity and impact. What remains unclear is whether …
Surface Roughness Influence on CPE Parameters in Electrolytic Cells
We investigate how the changes on the electrode surface may influence the behavior of the constant–phase elements (CPE) and, …
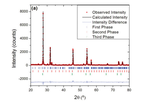
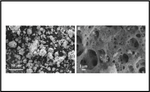
Structural characterization of (Bi1-xGdx)14W2O27 (x = 0.00 and 0.05) synthesized via mechano-thermal treatment
Samples of (Bi1-xGdx)14W2O27 (x = 0 and 0.05) compounds were prepared via a combination of mechanochemical and thermal treatments upon …
Discriminating image textures with the multiscale two-dimensional complexity-entropy causality plane
The aim of this paper is to further explore the usefulness of the two-dimensional complexity-entropy causality plane as a texture image …
Extensive Characterization of Seismic Laws in Acoustic Emissions of Crumpled Plastic Sheets
Statistical similarities between earthquakes and other systems that emit cracking noises have been explored in diverse contexts, …
Fractional diffusion equations coupled by reaction terms
We investigate the behavior for a set of fractional reaction–diffusion equations that extend the usual ones by the presence of spatial …
The advantage of playing home in NBA: microscopic, team-specific and evolving features
The idea that the success rate of a team increases when playing home is broadly accepted and documented for a wide variety of sports. …
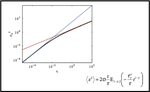
Transient superdiffusion and long-range correlations in the motility patterns of trypanosomatid flagellate protozoa
We report on a diffusive analysis of the motion of flagellate protozoa species. These parasites are the etiological agents of neglected …
Rural to urban population density scaling of crime and property transactions in English and Welsh Parliamentary Constituencies
Urban population scaling of resource use, creativity metrics, and human behaviors has been widely studied. These studies have not …
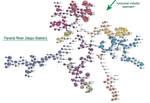
Characterization of river flow fluctuations via horizontal visibility graphs
We report on a large-scale characterization of river discharges by employing the network framework of the horizontal visibility graph. …
Solutions for a sorption process governed by a fractional diffusion equation
We investigate a sorption process where one substance spreads out through another having possibility of chemical reaction between them. …
Electrolytic cell containing different groups of ions with anomalous diffusion approach
The electrical response of an electrolytic cell containing more than one group of ions is investigated under the fractional approach …
Scale-adjusted metrics for predicting the evolution of urban indicators and quantifying the performance of cities
More than a half of world population is now living in cities and this number is expected to be two-thirds by 2050. Fostered by the …
Solutions for a fractional diffusion equation: Anomalous diffusion and adsorption-desorption processes
We investigate the solutions of a fractional diffusion equation subjected to boundary conditions which can be connected to adsorption – …
Solutions for a fractional diffusion equation with radial symmetry and integro-differential boundary conditions
The solutions for a dimensional system with radial symmetry and governed by a fractional diffusion equation have been investigated. …
Temperature dependence of refractive index and of electrical impedance of grape seed (Vitis vinifera, Vitis labrusca) oils extracted by Soxhlet and mechanical pressing
In this report, the temperature dependence of the refractive index and electric impedance of vegetable oil grape seeds extracted from …
Analogies between the cracking noise of ethanol-dampened charcoal and earthquakes
We report on an extensive characterization of the cracking noise produced by charcoal samples when dampened with ethanol. We argue that …
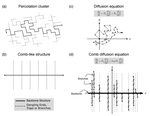
Spatial correlations, clustering and percolation-like transitions in homicide crimes
The spatial dynamics of criminal activities has been recently studied through statistical physics methods; however, models and results …
Non-Gaussian center-of-pressure velocity distribution during quiet stance
In the present study, we investigate patterns in the postural sway that characterize the static balance in human beings. To measure the …
We need more empirical investigations and model validation for a better understanding of crime - Comment on 'Statistical physics of crime: A review' by M.R. D'Orsogna and M. Perc
Since the seminal works of Wilson and Kelling [1] in 1982, the “broken windows theory” seems to have been widely accepted among the …
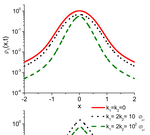
Unusual diffusing regimes caused by different adsorbing surfaces
A confined liquid with dispersed neutral particles is theoretically studied when the limiting surfaces present different dynamics for …
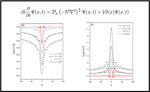
Solutions for a q-generalized Schrödinger equation of entangled interacting particles
We report on the time dependent solutions of the $q$-generalized Schrödinger equation proposed by Nobre et al. (2011). Here we …
Very prolonged practice in block of trials: Scaling of fitness, universality and persistence
In this study, we analyze the reaction times obtained from participants in a psychomotor activity composed of a large number of trials …
Growth Patterns and Scaling Laws Governing AIDS Epidemic in Brazilian Cities
Brazil holds approximately 1/3 of population living infected with AIDS (acquired immunodeficiency syndrome) in Central and South …
Fractional diffusion equation, boundary conditions and surface effects
We investigate a system governed by a fractional diffusion equation with an integro-differential boundary condition on the surface. …
Investigating the interplay between mechanisms of anomalous diffusion via fractional Brownian walks on a comb-like structure
The comb model is a simplified description for anomalous diffusion under geometric constraints. It represents particles spreading out …
Reaction on a solid surface supplied by an anomalous mass transfer source
The reaction process occurring on a solid surface where active sites are present is investi- gated. The phenomenon is described by a …
Empirical analysis on the connection between power-law distributions and allometries for urban indicators
We report on the existing connection between power-law distributions and allometries. As it was first reported in Gomez-Lievano et al. …
Universal bursty behaviour in human violent conflicts
Understanding the mechanisms and processes underlying the dynamics of collective violence is of considerable current interest. Recent …
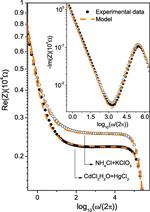
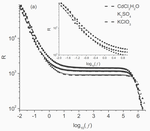
Fractional Diffusion Equations and Equivalent Circuits Applied to Ionic Solutions
We investigate dilute solutions of different salts (KClO3, K2SO4, and CdCl2H2O) dissolved in Milli-Q deionized water in the context of …
Long-range spatial correlations and fluctuation statistics of lightning activity rates in Brazil
We report on a statistical analysis of the lightning activity rates in all Brazilian cities. We find out that the average of lightning …
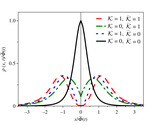
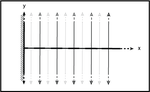
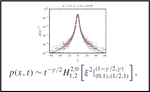
First passage time for a diffusive process under a geometric constraint
We investigate the solutions, survival probability, and first passage time for a two dimensional diffusive process subjected to the …
Engagement in the electoral processes: Scaling laws and the role of the political positions
| PDF
We report on a statistical analysis of the engagement in the electoral processes of all Brazilian cities by considering the …
Time dependent solutions for a fractional Schrödinger equation with delta potentials
We investigate, for an arbitrary initial condition, the time dependent solutions for a fractional Schrödinger equation in presence of …
Distance to the scaling law: a useful approach for unveiling relationships between crime and urban metrics
We report on a quantitative analysis of relationships between the number of homicides, population size and other ten urban metrics. By …
The transformation groupoid structure of the q-Gaussian family
Groupoid theory plays an important role in physics since the beginnings of quantum mechanics. Recent developments in understanding …
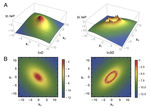
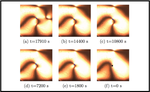
Antipersistent behavior of defects in a lyotropic liquid crystal during annihilation
We report on the dynamical behavior of defects of strength s = +/- 1/2 in a lyotropic liquid crystal during the annihilation process. …
Annihilation dynamics of stringlike topological defects in a nematic lyotropic liquid crystal
Topological defects can appear whenever there is some type of ordering. Its ubiquity in nature has been the subject of several studies, …
Scaling laws in the dynamics of crime growth rate
The increasing number of crimes in areas with large concentrations of people have made cities one of the main sources of violence. …
Diffusive process on a backbone structure with drift terms
The effects of an external force on a diffusive process subjected to a backbone structure are investigated by considering the system …
Move-by-move dynamics of the advantage in chess matches reveals population-level learning of the game
The complexity of chess matches has attracted broad interest since its invention. This complexity and the availability of large number …
Anomalous Diffusion and Electrical Response of Ionic Solutions
We analyze the electrical response obtained in the framework of a model in which the diffusion of mobile ions in the bulk is governed …
Anomalous diffusion and long-range correlations in the score evolution of the game of cricket
We investigate the time evolution of the scores of the second most popular sport in the world: the game of cricket. By analyzing, event …
Continuous Time Random Walk and different diffusive regimes
We investigate how it is possible to obtain different diffusive regimes from the Continuous Time Random Walk (CTRW) approach performing …
Anomalous Decay in Short Time Response of Ternary Mixtures with Ferrofluid
We study the optical transmittance of ternary mixtures of water, glycerin and ferrofluids. These mix- tures are subject to pulsed …
Complexity-Entropy Causality Plane as a Complexity Measure for Two-Dimensional Patterns
Complexity measures are essential to understand complex systems and there are numerous definitions to analyze one- dimensional data. …
Fractional Diffusion Equation and the Electrical Impedance: Experimental Evidence in Liquid-Crystalline Cells
The electrical impedance data of different nematic liquid-crystal cells are analyzed in the framework of a model in which the diffusion …
Scale-invariant structure of size fluctuations in plants
A wide range of physical and biological systems exhibit complex behaviours characterised by a scale-invariant structure of the …
Solutions for a fractional diffusion equation with noninteger dimensions
We investigate a fractional diffusion equation with a nonlocal reaction term by using the Green function approach. We also consider a …
Different diffusive regimes, generalized Langevin and diffusion equations
We investigate a generalized Langevin equation (GLE) in the presence of an additive noise characterized by the mixture of the usual …
Fractional Schrodinger equation with noninteger dimensions
The spatial and time dependent solutions of the Schrödinger equation incorporating the fractional time derivative of distributed order …
Complexity-entropy causality plane: A useful approach for distinguishing songs
Nowadays we are often faced with huge databases resulting from the rapid growth of data storage technologies. This is particularly true …
Extensive-like and intensive-like thermodynamical variables in generalized thermostatistics
We study a system of interacting particles in the framework of the two-parameter Sharma–Mittal entropy Sq,r. The two-body Hamiltonian …
Anomalous-diffusion approach applied to the electrical response of water
We investigate the electrical response of Milli-Q deionized water by using a fractional diffusion equation of distributed order with …
Anomalous diffusion and memory effects on the impedance spectroscopy for finite-length situations
The contribution of ions to the electrical impedance of an electrolytic cell limited by perfect blocking electrodes is determined by …
Scaling laws and universality in the choice of election candidates
Nowadays there is an increasing interest of physicists in finding regularities related to social phenomena. This interest is clearly …
Anomalous diffusion governed by a fractional diffusion equation and the electrical response of an electrolytic cell
The electrical response of an electrolytic cell in which the diffusion of mobile ions in the bulk is governed by a fractional diffusion …
Exact propagator for a Fokker-Planck equation, first passage time distribution, and anomalous diffusion
We obtain an exact form for the propagator of the Fokker-Planck equation in presence of the external force. Using the results found …
Non-Markovian diffusion equation and diffusion in a porous catalyst
We revisit the problem of diffusion in a porous catalyst by incorporating in the diffusion equation fractional time derivatives and a …
Identifying and modeling patterns oftetrapod vertebrate mortality rates in the Gulf of Mexico oil spill
The accidental oil spill in the Gulf of Mexico in 2010 has caused perceptible damage to marine and freshwater ecosystems. The large …
Finite-size effect on the surface deformation thermal mirror method
The finite-size effect on the thermal mirror (TM) experiments is described. The time-resolved thermoelastic deformation equation is …
Anomalous diffusion in a symbolic model
In this work, we investigate some statistical properties of symbolic sequences generated by a numerical procedure in which the symbols …
Comparison of Impedance Spectroscopy Expressions and Responses of Alternate Anomalous Poisson-Nernst-Planck Diffusion Equations for Finite-Length Situations
Two empirical, but plausible, previously published independent generalizations of the standard Poisson-Nernst-Planck (PNP) continuum …
Spreading Patterns of the Influenza A (H1N1) Pandemic
We investigate the dynamics of the 2009 influenza A (H1N1/S-OIV) pandemic by analyzing data obtained from World Health Organization …
Solutions for a diffusion equation with a backbone term
We investigate the diffusion equation subjected to the boundary conditions ρ(±∞, y;t) = 0 and ρ(x,±∞;t) = 0, and the initial condition …
The soundscape dynamics of human agglomeration
We report on a statistical analysis of the people agglomeration soundscape. Specifically, we investigate the normalized sound amplitudes …
On the dynamics of bubbles in boiling water
We investigate the dynamics of many interacting bubbles in boiling water by using a laser scattering experiment. Specifically, we …
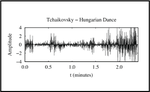
Universal patterns in sound amplitudes of songs and music genres
We report a statistical analysis of more than eight thousand songs. Specifically, we investigated the probability distribution of the …
Some results for an N-dimensional nonlinear diffusion equation with radial symmetry
The solutions of a nonlinear diffusion equation by considering the radially symmetric N-dimensional case are investigated. This …
Earthquake-like patterns of acoustic emission in crumpled plastic sheets
We report remarkable similarities in the output signal of two distinct out-of-equilibrium physical systems – earthquakes and the …
Solutions for a non-Markovian diffusion equation
Solutions for a non-Markovian diffusion equation are investigated. For this equation, we consider a spatial and time dependent …
Continuous-time random walk as a guide to fractional Schrödinger equation
We argue that the continuous-time random walk approach may be a useful guide to extend the Schrödinger equation in order to incorporate …
Surface viscosity and reorientation process in an asymmetric nematic cell
The influence of surface viscosity and anchoring energy on the reorientation process of a nematic liquid crystal cell is theoretically …
Identification of Biochemical Reactors Using Fractional Differential Equations
High production meeting product quality, process safety and environmental regulation provide to control systems a key role in …
Electrical impedance of an electrolytic cell in the presence of generation and recombination of ions
The electrical impedance of an insulating solid containing ions is evaluated in the presence of the generation and recombination of …
Fractional control of an industrial furnace
The requirements of high production allied with product quality, process safety and environmental regulation, lead control systems to …
A continuous time random walk model with multiple characteristic times
In this paper we consider a continuous time random walk (CTRW) model with a decoupled jump pdf. Further, we consider an approximate …
Dynamics of tournaments: the soccer case
A random walk-like model is considered to discuss statistical aspects of tournaments. The model is applied to soccer leagues with …
Analytical solution for mode-mismatched thermal lens spectroscopy with sample-fluid heat coupling
This paper presents an improved theoretical description of the mode-mismatched thermal lens effect using models that account for heat …
Critical exponents for Fréedericskz transition in nematics between concentric cylinders
The equilibrium tilt angle profile in a cell limited by two concentric cylinders filled with nematic liquid crystals is determined for …
Non-Markovian diffusion and the adsorption-desorption process
The non-Markovian diffusion of dispersed particles in a semi-infinite cell of an isotropic fluid limited by an adsorbing-desorbing …
Influence of the anchoring energy on the relaxation of the nematic deformation
We analyze the influence of the anchoring energy strength on the relaxation of the nematic deformation, when the distorting field is …
Fokker-Planck equation in a wedge domain: Anomalous diffusion and survival probability
We obtain exact solutions and the survival probability for a Fokker-Planck equation subjected to the two-dimensional wedge domain. We …
Green function for a non-Markovian Fokker-Planck equation: Comb-model and anomalous diffusion
We investigate solutions, by using the Green function approach, for a system governed by a non-Markovian Fokker-Planck equation and …
Symbolic Sequences and Tsallis Entropy
We address this work to investigate symbolic sequences with long-range correlations by using computational simulation. We analyze …
Fractional Diffusion Equation and Impedance Spectroscopy of Electrolytic Cells
The influence of the ions on the electrochemical impedance of a cell is calculated in the framework of a complete model in which the …
Nonlocal effects on the thermal behavior of non-crystalline solids
We argue that nonlocal effects represented by fractionary terms in the kinetic energy can be relevant to achieve a satisfactory …
Solutions for diffusion equation with a nonlocal term
This work is devoted to investigating solutions for the diffusion equation with a nonlocal spatial and time-dependent term by using the …
Director profile of a nematic between two concentric cylinders with inhomogeneous boundary conditions
The tilt angle profile in a nematic cell limited by two concentric cylindrical surfaces with inhomogeneous distribution of easy axes is …
q-distributions in complex systems: a brief review
The nonextensive statistical mechanics proposed by Tsallis is today an intense and growing research field. Probability distributions …
Solutions for a fractional nonlinear diffusion equation with external force and absorbent term
We devote this work to investigate the solutions of a N-dimensional nonlinear fractional diffusion equation which emerges from the …
Generalized entropy indices to measure α- and β-diversities of macrophytes
A family of entropy indices constructed in the framework of Tsallis entropy formalism is used to investigate ecological diversity. It …
Some results for a fractional diffusion equation with radial symmetry in a confined region
We investigate an N-dimensional fractional diffusion equation with radial symmetry by taking a spatial and time dependent diffusion …
Anomalous diffusion and the adsorption-desorption process in anisotropic media
The diffusive process of dispersed particles in a semi-infinite cell of an anisotropic fluid limited by an adsorbing surface is …