Abstract
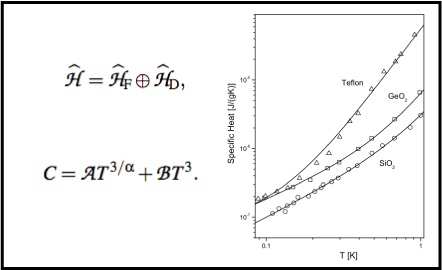
We argue that nonlocal effects represented by fractionary terms in the kinetic energy can be relevant to achieve a satisfactory phenomenological description of the thermal behavior of the specific heat of non-crystalline solids at very low temperature. We propose a simple model formed by the direct sum of two Hamiltonians, one of which is obtained by incorporating fractional derivatives in the kinetic energy of a conventional Hamiltonian, and the other one accounts for the presence of phonons in the system. Some experimental data are used to support the proposed description.
Type