Abstract
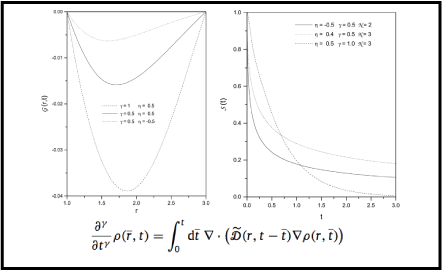
We investigate an N-dimensional fractional diffusion equation with radial symmetry by taking a spatial and time dependent diffusion coefficient into account, i.e., D(r,t) = D(t)r^(-n) with D(t) = D delta(t) + D(t). The equation is considered in a confined region and subjected to time dependent boundary conditions which may be related to inhomogeneous characteristics of the surfaces confining the system. The results show an anomalous spreading of the solutions and an unusual behavior of the survival probability.
Type