Abstract
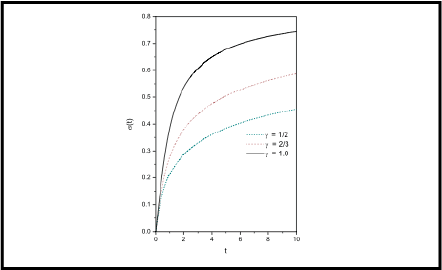
The non-Markovian diffusion of dispersed particles in a semi-infinite cell of an isotropic fluid limited by an adsorbing-desorbing surface is theoretically investigated. The density of dispersed particles in the bulk is a time dependent function and the time dependent density of surface particles is governed by a modified kinetic equation with a time dependent kernel. In this framework, the densities of bulk and surface particles are analytically determined, taking into account the conservation of the number of particles immersed in the sample. This system exhibits anomalous diffusion behavior as well as memory effects in the adsorption- desorption process. The results obtained here are expected to be useful to investigate the adsorption-desorption phenomena of neutral as well as charged particles in an isotropic fluid in contact with a solid substrate when the anomalous diffusion is present.