Comparison of Impedance Spectroscopy Expressions and Responses of Alternate Anomalous Poisson-Nernst-Planck Diffusion Equations for Finite-Length Situations

Abstract

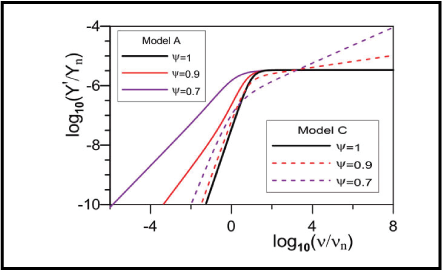
Two empirical, but plausible, previously published independent generalizations of the standard Poisson-Nernst-Planck (PNP) continuum illusion model for mobile-charge conduction in liquids and solids are discussed, their responses are compared, and their physical appropriateness and usefulness for data fitting are investigated. They both involve anomalous diffusion of PNPA type with power-law frequency-response elements involving fractional exponents. Both models apply to finite-length regions of material between completely blocking electrodes and, for simplicity, deal primarily with positive and negative charge carriers of equal valence numbers and mobilities. The charge carriers may be either ionic or electronic. The first PNPA model, model A, involves the common separation of the expression for ordinary PNP impedance into an interface diffusion part and a high-frequency limiting conductance and capacitance, followed by the replacement of all normal diffusion elements in the former by anomalous ones. It predicts the presence of the usual PNP plateau in the real part of the total impedance below the Debye relaxation frequency, followed at sufficiently low frequencies by an anomalous-diffusion power-law increase above the plateau. The second model, C, alternatively generalizes the normal time derivatives in the continuity equation by replacing them with fractional ones and leads to no plateau, except in the PNP limit, but instead predicts an immediate power-law increase as the frequency decreases below the Debye relaxation one. Fitting of experimental frequency response data sets for three disparate materials leads to much poorer fits for model C than for model A.