Anomalous diffusion and long-range correlations in the score evolution of the game of cricket
Abstract
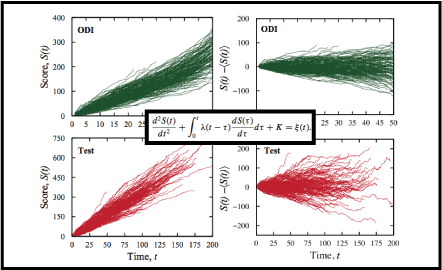
We investigate the time evolution of the scores of the second most popular sport in the world: the game of cricket. By analyzing, event by event, the scores of more than 2000 matches, we point out that the score dynamics is an anomalous diffusive process. Our analysis reveals that the variance of the process is described by a power-law dependence with a superdiffusive exponent, that the scores are statistically self-similar following a universal Gaussian distribution, and that there are long-range correlations in the score evolution. We employ a generalized Langevin equation with a power-law correlated noise that describes all the empirical findings very well. These observations suggest that competition among agents may be a mechanism leading to anomalous diffusion and long-range correlation.