Extensive-like and intensive-like thermodynamical variables in generalized thermostatistics

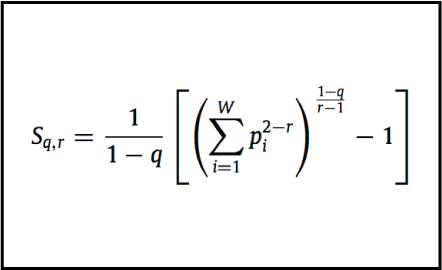
Abstract

We study a system of interacting particles in the framework of the two-parameter Sharma–Mittal entropy Sq,r. The two-body Hamiltonian describing the interaction between the particles of the system is obtained requiring that the equilibrium distribution can be factorized in the product of the distributions of the single particles. In the present picture, we derive, according to the zeroth principle of thermodynamics, a possible definition of temperature and pressure and investigate their scaling properties. We show that, if the parameter q scales according to the law q′ − 1 = λ (q − 1), temperature and pressure are intensive-like quantities, while entropy has an extensive-like behavior.