Fractional Diffusion Equation and the Electrical Impedance: Experimental Evidence in Liquid-Crystalline Cells

Abstract

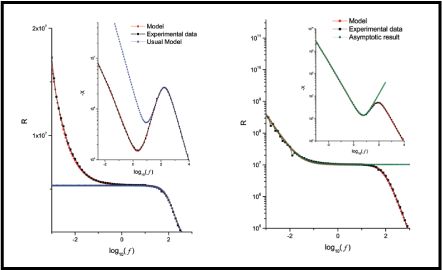
The electrical impedance data of different nematic liquid-crystal cells are analyzed in the framework of a model in which the diffusion of mobile ions in the bulk is governed by a fractional diffusion equation of distributed order. The boundary conditions at the electrodes limiting the sample are described by an integro-differential equation governing the kinetic at the interface that embodies, in particular, the usual kinetic equation for describing the adsorption−desorption process at the electrodes but is expressed in terms of a temporal kernel that can be chosen to cover scenarios that are not suitably described within the usual framework of blocking electrodes. The analysis is carried out by supposing that the positive and negative ions have the same mobility and that the electric potential profile across the sample satisfies the Poisson’s equation. The results cover a rich variety of scenarios, including the ones connected to anomalous diffusion.