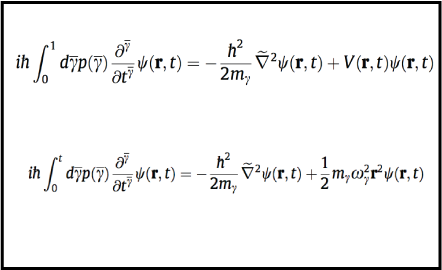
Abstract
The spatial and time dependent solutions of the Schrödinger equation incorporating the fractional time derivative of distributed order and extending the spatial operator to noninteger dimensions are investigated. They are obtained by using the Green function approach in two situations: the free case and in the presence of a harmonic potential. The results obtained show an anomalous spreading of the wave packet which may be related to an anomalous diffusion process.
Type