Abstract
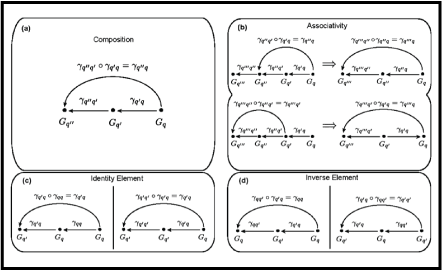
Groupoid theory plays an important role in physics since the beginnings of quantum mechanics. Recent developments in understanding symmetries in complex dynamical systems underpin the growing importance of groupoid theory also for statistical mechanics. The q-Gaussian function is observed as the distribution function of many physical and biological systems and emerges naturally in the statistical mechanics of non-ergodic and complex systems. A number of dynamical systems are characterized by pairs and triples of q-Gaussians. The aim of this work is to relate these triples of q-Gaussians with different q-values, representing intrinsic symmetries of the dynamical system at hand, such that any value of q can be mapped uniquely to any other value q′. We present a complete set of transformations of q-Gaussians by deriving a general map γqq′ that transforms normalizable q-Gaussian distributions into one another. We show that the action of γqq′ is a transformation groupoid.