Solutions for a fractional diffusion equation with radial symmetry and integro-differential boundary conditions

Abstract

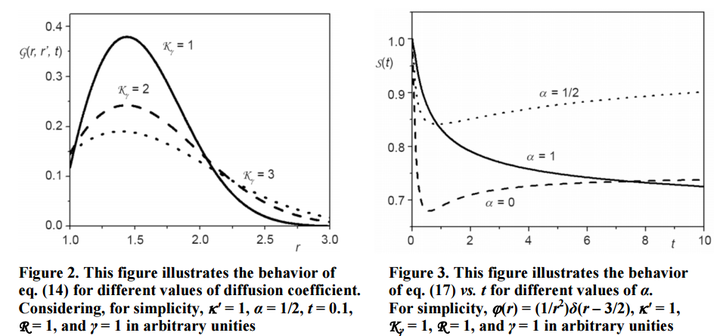
The solutions for a dimensional system with radial symmetry and governed by a fractional diffusion equation have been investigated. More specifically, a spherical system was considered, being defined in the semi - infinity interval [R, ¥) and subjected to surface effects described in terms of integro - differential boundary conditions which has many practical applications. The analytical solutions were obtained by using the Green function approach, showing a broad range of different behaviors which can be related to anomalous diffusion. The analyses also considered the influence of the parameters of the analytical solution in order to describe a more realistic scenario.