Anomalous diffusion and transport in heterogeneous systems separated by a membrane

Abstract

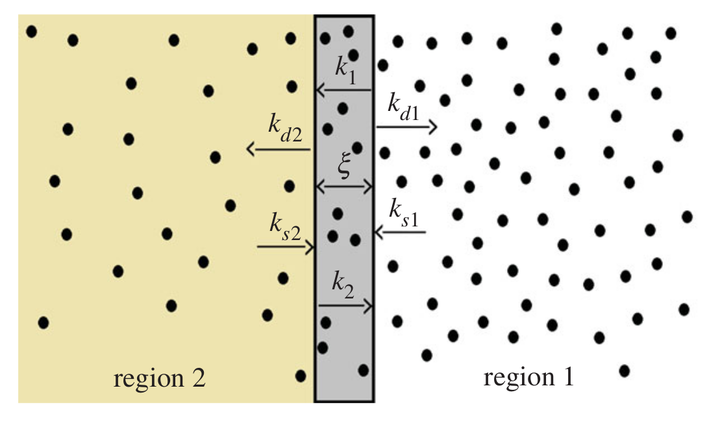
Diffusion of particles in a heterogeneous system separated by a semipermeable membrane is investigated. The particle dynamics is governed by fractional diffusion equations in the bulk and by kinetic equations on the membrane, which characterizes an interface between two different media. The kinetic equations are solved by incorporating memory effects to account for anomalous diffusion and, consequently, non-Debye relaxations. A rich variety of behaviours for the particle distribution at the interface and in the bulk may be found, depending on the choice of characteristic times in the boundary conditions and on the fractional index of the modelling equations.