Asymptotic behaviors of the Poisson-Nernst-Planck model, generalizations and best adjust of experimental data

Abstract

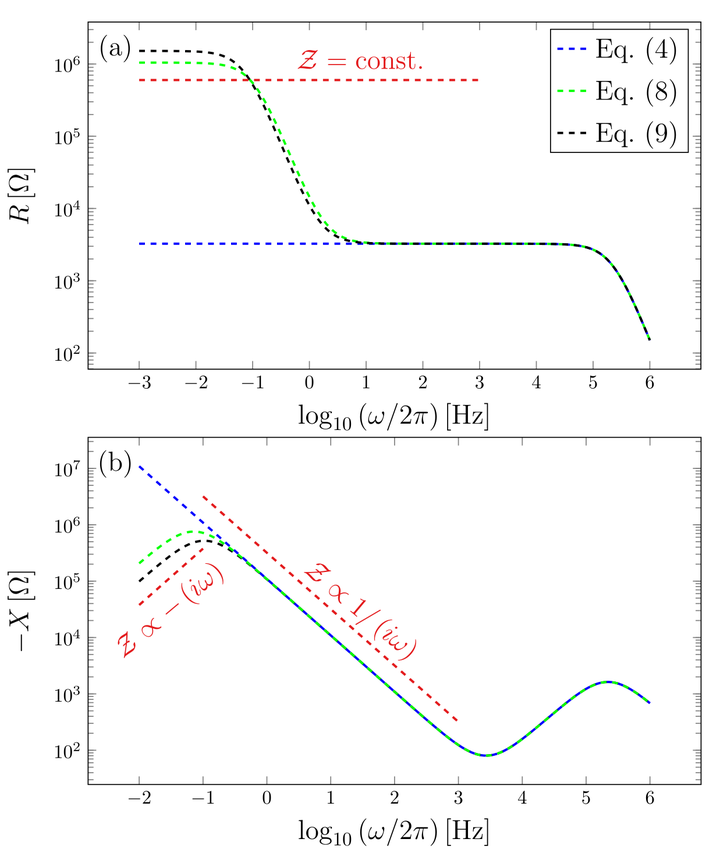
We analyze the asymptotic behavior of the impedance (or immittance) spectroscopy response of an electrolytic cell in a finite-length situation obtained from the Poisson-Nernst-Planck (PNP) diffusional model and extensions by taking into account different surface effects. The analysis starts with the case characterized by perfect blocking electrodes and proceeds by considering non-blocking conditions on electrodes surface. We argue that the imaginary part of the impedance may be directly related to the boundary condition on the electrode surface, such as charge accumulation and/or transfer by electrochemical reaction or adsorption-desorption processes. We also compare the theoretical predictions with experimental data obtained for a weak electrolytic solution of KClO3.