Characterizing Time Series via Complexity-Entropy Curves

Abstract

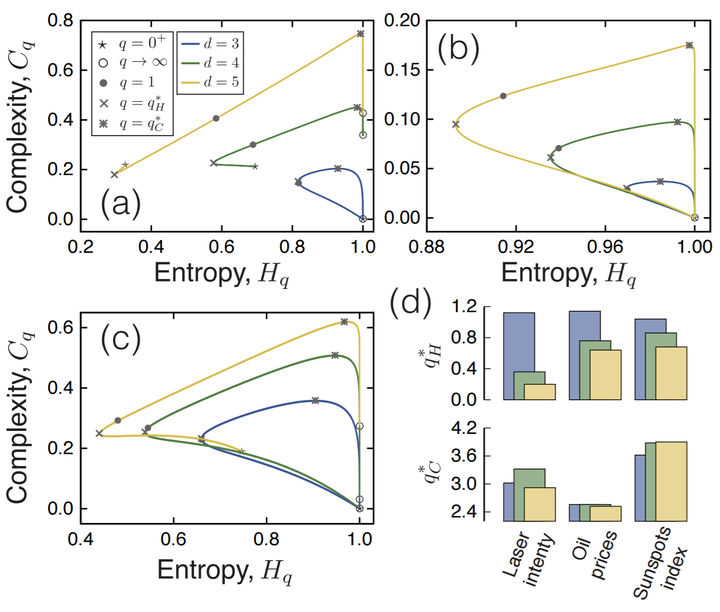
The search for patterns in time series is a very common task when dealing with complex systems. This is usually accomplished by employing a complexity measure such as entropies and fractal dimensions. However, such measures usually only capture a single aspect of the system dynamics. Here, we propose a family of complexity measures for time series based on a generalization of the complexity-entropy causality plane. By replacing the Shannon entropy by a mono-parametric entropy (Tsallis q-entropy) and after considering the proper generalization of the statistical complexity (q-complexity), we build up a parametric curve (the q-complexity-entropy curve) that is used for characterizing/classifying time series. Based on simple exact results and numerical simulations of stochastic processes, we show that these curves can distinguish among different long-range, short-range and oscillating correlated behaviors. Also, we verify that simulated chaotic and stochastic time series can be distinguished based on whether these curves are open or closed. We further test this technique in experimental scenarios related to chaotic laser intensity, stock price, sunspot, and geomagnetic dynamics, confirming its usefulness. Finally, we prove that these curves enhance the automatic classification of time series with long-range correlations and interbeat intervals of healthy subjects and patients with heart disease.