Abstract
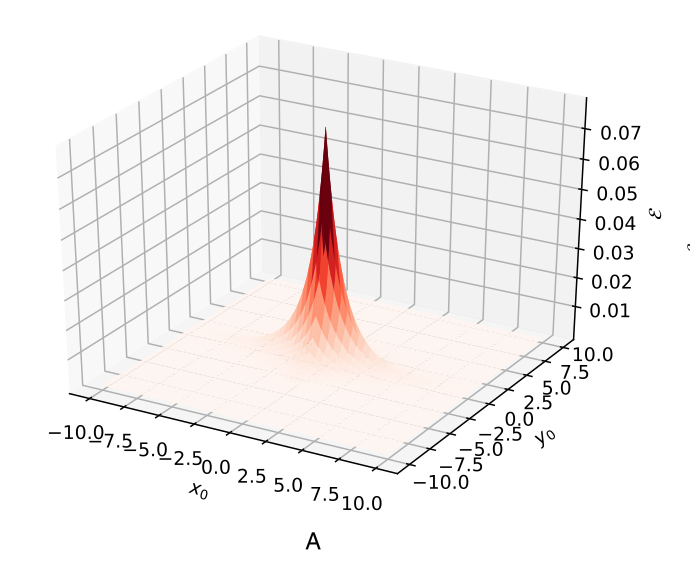
We present an analytical treatment of anomalous diffusion in a three-dimensional comb (xyz-comb) by using the Green’s function approach. We derive exact analytical solutions for the propagators for an instantaneous point injection and natural boundary conditions. The marginal distributions for all three directions are obtained and the corresponding mean squared displacements are found. The analytical results are confirmed by numerical simulations in the framework of coupled Langevin equations. We also analyze a random search process on the xyz-comb, and analytical results on the first arrival time distribution, search reliability and efficiency are obtained. Results for multiple targets are presented as well. The developed approach can be useful for further studies of the Brownian–Lévy searches in the xyz-comb, and analysis of optimal search strategies on comb-like structures.