Quenched and Annealed Disorder Mechanisms in Comb-Models with Fractional Operators

Abstract

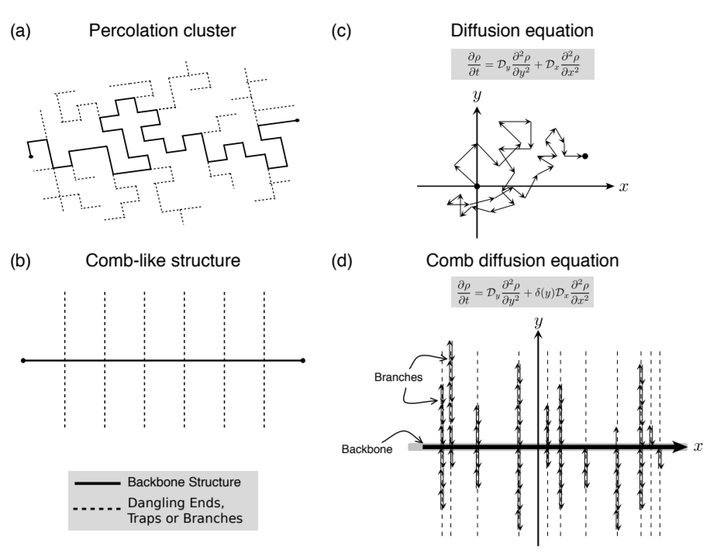
Recent experimental findings on anomalous diffusion have demanded novel models that combine annealed (temporal) and quenched (spatial or static) disorder mechanisms. The comb-model is a simplified description of diffusion on percolation clusters, where the comb-like structure mimics quenched disorder mechanisms and yields a subdiffusive regime. Here we extend the comb-model to simultaneously account for quenched and annealed disorder mechanisms. To do so, we replace usual derivatives in the comb diffusion equation by different fractional time-derivative operators and the conventional comb-like structure by a generalized fractal structure. Our hybrid comb-models thus represent a diffusion where different comb-like structures describe different quenched disorder mechanisms, and the fractional operators account for various annealed disorders mechanisms. We find exact solutions for the diffusion propagator and mean square displacement in terms of different memory kernels used for defining the fractional operators. Among other findings, we show that these models describe crossovers from subdiffusion to Brownian or confined diffusions, situations emerging in empirical results. These results reveal the critical role of interactions between geometrical restrictions and memory effects on modeling anomalous diffusion.