Abstract
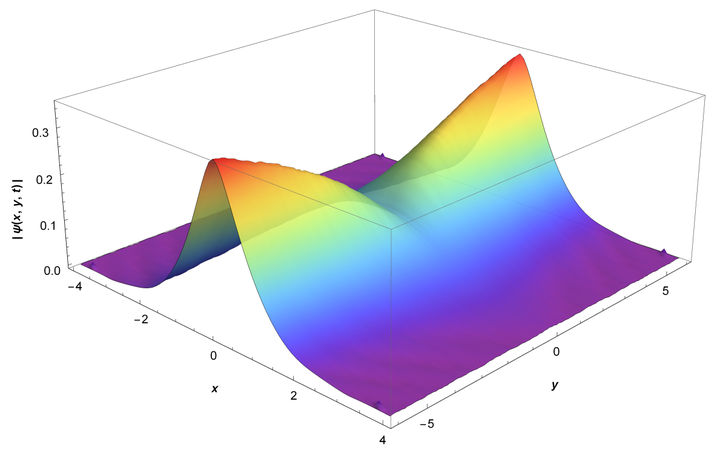
We investigate the solutions of the Schrödinger equation in the presence of geometric constraints represented by a backbone structure and by taking into account a position-dependent effective mass. The new solutions are obtained by using Green’s function approach, and the results are given in terms of stretched exponential functions, which may be linked to the fractal properties of the media and connected with an anomalous spreading of the wave-packet. The interplay introduced by a backbone structure constraining the different directions is also analyzed, showing their mutual influence in the dynamics of the quantum system underlying the analysis. In addition, we also discuss connections between the heterogeneity promoted by the comb-model and the effective mass with a fractional Schrödinger equation.