Abstract
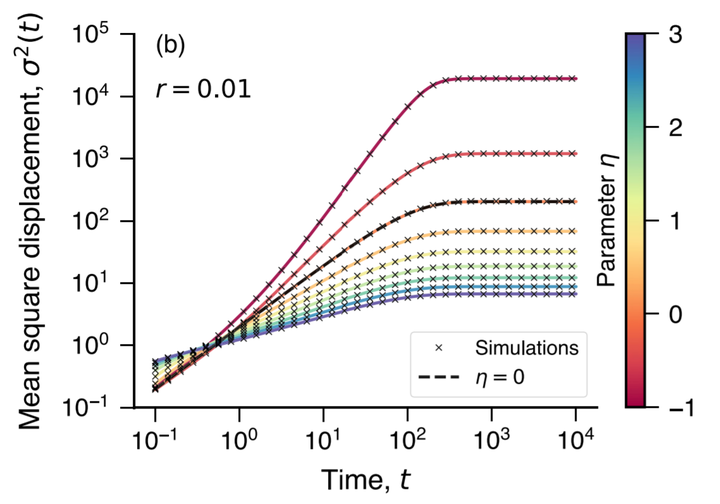
We investigate a diffusion process in heterogeneous media where particles stochastically reset to their initial positions at a constant rate. The heterogeneous media is modeled using a spatial-dependent diffusion coefficient with a power-law dependence on particles’ positions. We use the Green function approach to obtain exact solutions for the probability distribution of particles’ positions and the mean square displacement. These results are further compared and agree with numerical simulations of a Langevin equation. We also study the first-passage time problem associated with this diffusion process and obtain an exact expression for the mean first-passage time. Our findings show that this system exhibits non-Gaussian distributions, transient anomalous diffusion (sub- or superdiffusion) and stationary states that simultaneously depend on the media heterogeneity and the resetting rate. We further demonstrate that the media heterogeneity non-trivially affect the mean first-passage time, yielding an optimal resetting rate for which this quantity displays a minimum.