Abstract
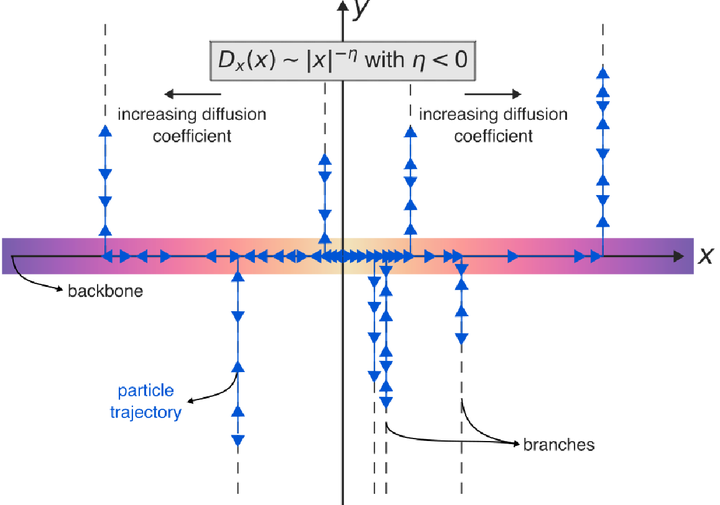
Heterogeneous media diffusion is often described using position-dependent diffusion coefficients and estimated indirectly through mean squared displacement in experiments. This approach may overlook other mechanisms and their interaction with position-dependent diffusion, potentially leading to erroneous conclusions. Here, we introduce a hybrid diffusion model that merges a position-dependent diffusion coefficient with the trapping mechanism of the comb model. We derive exact solutions for position distributions and mean squared displacements, validated through simulations of Langevin equations. Our model shows that the trapping mechanism attenuates the impact of media heterogeneity. Superdiffusion occurs when the position-dependent coefficient increases superlinearly, while subdiffusion occurs for sublinear and inverse power-law relations. This nontrivial interplay between heterogeneity and state-independent mechanisms also leads to anomalous yet Brownian, and non-Brownian yet Gaussian regimes. These findings emphasize the need for cautious interpretations of experiments and highlight the limitations of relying solely on mean squared displacements or position distributions for diffusion characterization.