A heteroscedastic Bayesian generalized logistic regression model with application to scaling problems
Abstract
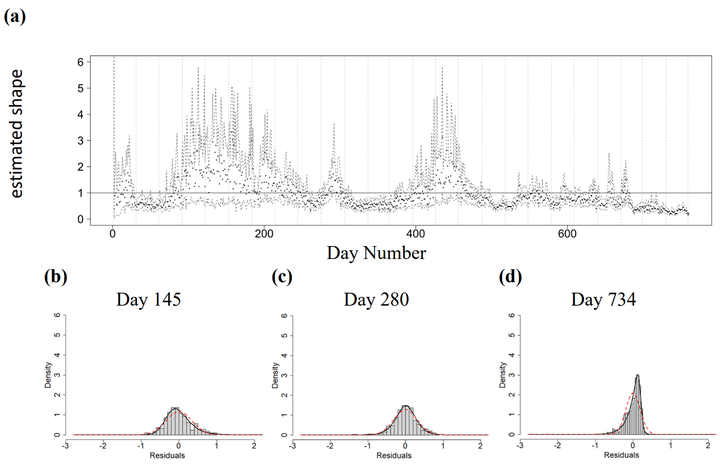
Power law scaling models have been used to understand the complexity of systems as diverse as cities, neurological activity, and rainfall and lightning. In the scaling framework, power laws and standard linear regression methods are widely used to estimate model parameters with assumed normality and fixed variance. Generalized linear models (GLM) can accommodate a wider range of distributions where the chosen distribution must meet the assumptions of the data to prevent model bias. We present a widely applicable Bayesian generalized logistic regression (BGLR) framework to more flexibly model a continuous real response addressing skew and heteroscedasticity. The Generalized Logistic Distribution (GLD) was selected to flexibly model skewed continuous data. This resulted in a nonlinear posterior distribution which may not have an analytical solution which can be solved numerically with Markov Chain Monte Carlo (MCMC) methods. We compared the BGLR model to standard and Bayesian normal models having fixed and varying variance when fitting power laws to 759 days of COVID-19 data. The BGLR yielded information beyond existing methods about the evolution of skew and skedasticity while revealing parameter bias of widely used methods. The BGLR flexibly modelled the complex characteristics necessary for an improved understanding of the propagation and dynamics of this infectious disease. The model is generally applicable and can be used as a template for modeling complexity with other distributions.