Diffusion in comb-structured surfaces coupled to bulk processes

Abstract

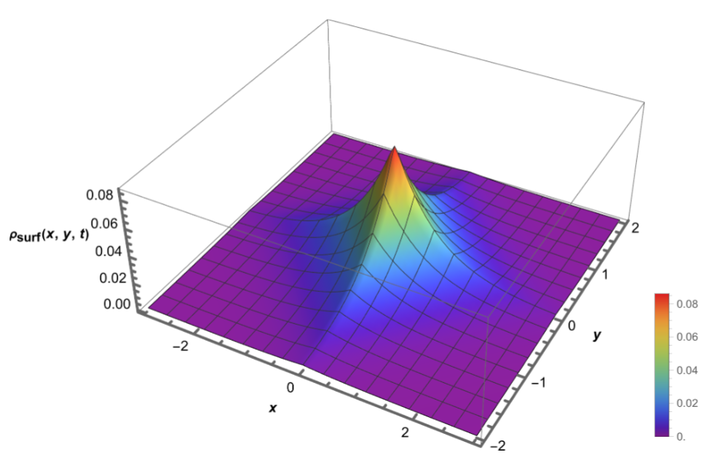
From the analytical perspective, we investigate the diffusion processes that arise from a system composed of a surface with a backbone structure coupled to the bulk via the boundary conditions. The problem is formulated in terms of diffusion equations with nonlocal terms, which can be used to model different processes, such as sorption–desorption and reactions on the surface. For the backbone structure, we consider the comb model, which imposes constraints on the diffusion processes in different directions on the surface. The results reveal abroad class of behaviors that can be connected to anomalous diffusion.