Symbolic Sequences and Tsallis Entropy

Abstract

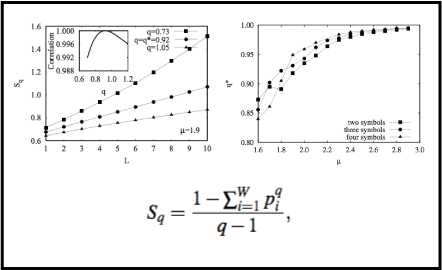
We address this work to investigate symbolic sequences with long-range correlations by using computational simulation. We analyze sequences with two, three and four symbols that could be repeated l times, with the probability distribution p(l) ∝ 1/(l^µ). For these sequences, we verified that the usual entropy increases more slowly when the symbols are correlated and the Tsallis entropy exhibits, for a suitable choice of q, a linear behavior. We also study the chain as a random walk-like process and observe a nonusual diffusive behavior depending on the values of the parameter µ.