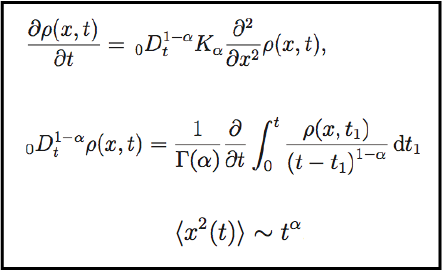
Abstract
In this paper we consider a continuous time random walk (CTRW) model with a decoupled jump pdf. Further, we consider an approximate jump length pdf; for the waiting time pdf we do not use any approximation and we employ a function which depends on multiple characteristic times given by a sum of exponential functions. This waiting time pdf can reproduce power-law behavior for intermediate times. Using this specific waiting time probability density, we analyze the behavior of the second moment generated by the CTRW model. It is known that the waiting time pdf given by an exponential function generates a normal diffusion process, but for our waiting time pdf the second moment can give an anomalous diffusion process for intermediate times, and the normal diffusion process is maintained for the long-time limit. We note that systems which present subdiffusive behavior for intermediate times but reach normal diffusion at large times have been observed in biology.