Critical exponents for Fréedericskz transition in nematics between concentric cylinders

Abstract

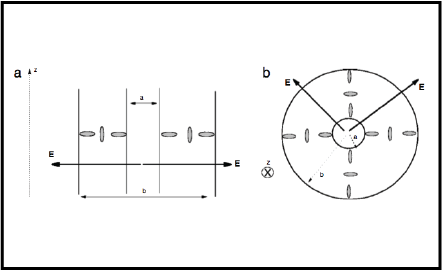
The equilibrium tilt angle profile in a cell limited by two concentric cylinders filled with nematic liquid crystals is determined for strong homeotropic anchoring at the surfaces. The anchoring condition is such that the nematic director is perpendicular to the cylinder axes and a radial nonuniform electric field is applied to investigate a Fréedericksz transition. The distortions induced by the field remain in the plane perpendicular to the cylinder axes, and a threshold field is analytically determined indicating a transition from a pure splay to a splay-bend conformation of the director. It is shown that this transition can be induced by the thickness of the region between the two cylinders, and can be detected even in the absence of an external field. If the maximum value of the tilt angle is assumed as an order parameter, its behavior near to the transition can be used to obtain the critical exponent, which is the same as the one obtained in the mean field approximation. These results are indications that nontrivial consequences may occur when complex fluids are subject to non-planar geometries.