Scaling laws and universality in the choice of election candidates

Abstract

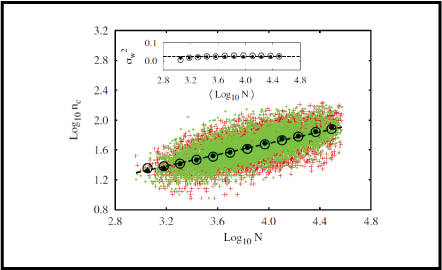
Nowadays there is an increasing interest of physicists in finding regularities related to social phenomena. This interest is clearly motivated by applications that a statistical mechanical description of the human behavior may have in our society. By using this framework, we address this work to cover an open question related to elections: the choice of elections candidates (candidature process). Our analysis reveals that, apart from the social motivations, this system displays features of traditional out-of-equilibrium physical phenomena such as scale-free statistics and universality. Basically, we found a non-linear (power law) mean correspondence between the number of candidates and the size of the electorate (number of voters), and also that this choice has a multiplicative underlying process (lognormal behavior). The universality of our findings is supported by data from 16 elections from 5 countries. In addition, we show that aspects of scale-free network can be connected to this universal behavior.