Solutions for a diffusion equation with a backbone term

Abstract

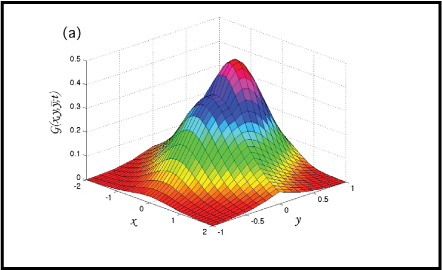
We investigate the diffusion equation subjected to the boundary conditions ρ(±∞, y;t) = 0 and ρ(x,±∞;t) = 0, and the initial condition ρ(x, y; 0) = ρ(x, y). We obtain exact solutions in terms of the Green function approach and analyze the mean square displacement in the x and y directions. This analysis shows an anomalous spreading of the system which is characterized by different diffusive regimes connected to anomalous diffusion.