Complexity-Entropy Causality Plane as a Complexity Measure for Two-Dimensional Patterns

Abstract

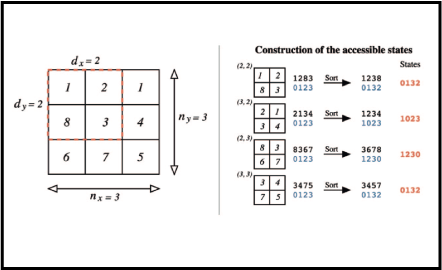
Complexity measures are essential to understand complex systems and there are numerous definitions to analyze one- dimensional data. However, extensions of these approaches to two or higher-dimensional data, such as images, are much less common. Here, we reduce this gap by applying the ideas of the permutation entropy combined with a relative entropic index. We build up a numerical procedure that can be easily implemented to evaluate the complexity of two or higher- dimensional patterns. We work out this method in different scenarios where numerical experiments and empirical data were taken into account. Specifically, we have applied the method to i) fractal landscapes generated numerically where we compare our measures with the Hurst exponent; ii) liquid crystal textures where nematic-isotropic-nematic phase transitions were properly identified; iii) 12 characteristic textures of liquid crystals where the different values show that the method can distinguish different phases; iv) and Ising surfaces where our method identified the critical temperature and also proved to be stable.