Solutions for a q-generalized Schrödinger equation of entangled interacting particles

Abstract

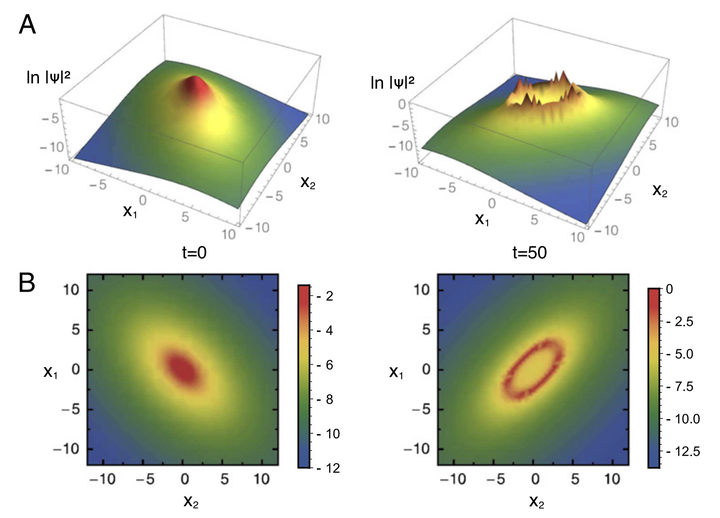
We report on the time dependent solutions of the $q$-generalized Schrödinger equation proposed by Nobre et al. (2011). Here we investigate the case of two free particles and also the case where two particles were subjected to a Moshinsky-like potential with time dependent coefficients. We work out analytical and numerical solutions for different values of the parameter $q$ and also show that the usual Schrödinger equation is recovered in the limit of $q o 1$. An intriguing behavior was observed for $q = 2$, where the wave function displays a ring-like shape, indicating a bind behavior of the particles. Differently from the results previously reported for the case of one particle, frozen states appear only for special combinations of the wave function parameters in case of $q = 3$.