Random Walks Associated with Nonlinear Fokker–Planck Equations

Abstract

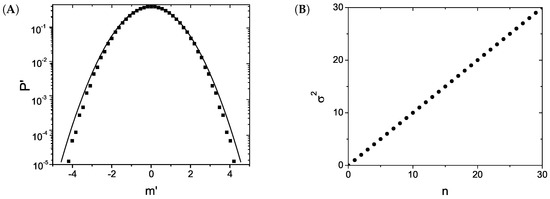
A nonlinear random walk related to the porous medium equation (nonlinear Fokker–Planck equation) is investigated. This random walk is such that when the number of steps is sufficiently large, the probability of finding the walker in a certain position after taking a determined number of steps approximates to a q-Gaussian distribution ( Gq,β(x)∝[1−(1−q)βx2]1/(1−q) ), which is a solution of the porous medium equation. This can be seen as a verification of a generalized central limit theorem where the attractor is a q-Gaussian distribution, reducing to the Gaussian one when the linearity is recovered ( q→1 ). In addition, motivated by this random walk, a nonlinear Markov chain is suggested.